Introduction:

One of the most important parameters in high frequency pipe and tube welding is the welding frequency. Yet, until recently, it has been one of the most misunderstood! Because no unified theory describing how frequency affects the weld area was available, most of what was known was based on empirical data and experiment. And because experimenting in a real pipe and tube mill environment is time consuming and difficult, much of the data available was incomplete and contradictory. A comprehensive theory for how frequency affects the high frequency welding process is now available and has been validated through experiment and comparison to actual tube welding data from numerous manufacturing operations. This theory describes how welding frequency affects:

• The Heat Distribution in the area of the weld “Vee".
• The Weld Power Requirement.
• The Size of the Heat Affected Zone (HAZ).
• The level of Magnetic Flux in the Impeder.

More importantly, the theory identifies the “optimum" welding frequency for a particular tube size, mill speed, and material.

This paper includes a minimum of mathematics with the aim of making it straight forward for the tube mill engineer to follow. Those interested in the details of the theory and its derivation should consult the paper cited in the end notes.

How the “Vee" Heats to the Forge Weld Temperature:

Let's consider the typical pipe and tubing, high frequency induction welding situation where the tube material is much thicker than an “Electrical Reference Depth" and an impeder is used that can support the required level of magnetic flux. This accounts for over 90% of the situations encountered in practice. Empirically, “how" the weld “vee" heats has been understood for a long time. High frequency current in the work coil induces a current in the opposite direction in the unwelded portion of the tube directly under the coil. This part of the process behaves as an electrical transformer in the sense that the portion of tube directly under the coil forms the single turn secondary of the transformer and the current is “stepped up" by the number of turns of the work coil. One of the functions of the impeder in the process is to form the “core" of the transformer. Thus, the magnetic flux that couples the current between the work coil and tube is essentially contained in the impeder. The current induced in the tube must flow in a closed electric circuit. When the current reaches the unwelded portion of the tube, a reasonable fraction flows along the “vee" edge to the apex and back closing the circuit with the current flowing around the tube, under the work coil. The current flows along the edge of the “vee" due to two physical phenomena:

• “The Classical Proximity Effect" which states that the magnetic field produced by a high frequency current flowing in one direction attracts a high frequency current flowing close to it in the opposite direction. As the high frequency currents on both sides of the “vee" are flowing in opposite directions, they tend to pull each other into the weld “vee".

• The “Surrogate Proximity Effect" in which a high frequency current in the presence of a magnetic field is attracted by the field. The physical laws of high frequency currents show that the equivalent surface current on a conductor equals the magnetic field flowing parallel to its surface. This in fact is the stronger effect in the weld “vee" as the total magnetic flux in the impeder must pass through the weld “vee" to close around the work coil.

The exact distribution of the current in the “vee" area is described by a set of physical laws called “Maxwell's Equations". The important consequence of these is that the current density, or the distribution of electric current in the “vee" material, can be found from:

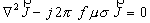1)

Where:

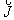	is the electrical current density in the pipe or tube material, ,
f	is the electrical welding frequency,
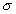	is the electrical conductivity of the pipe or tube material,
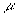	is the magnetic permeability of the pipe or tube material,
j	is is the square root of -1.

Solution of this equation shows that the current in a high frequency electrical system flows essentially on the surface of its conductors - the well known “Skin Effect". The highest concentration of current is at the surface of a conductor and as one moves into the conductor away from the surface, the current density reduces exponentially. The distance into the conductor at which the current density is e-1 or 0.368 times its value at the surface is called the “Electrical Reference Depth" and is determined by solving the equation above:

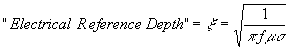2)

The current flowing in the “vee" dissipates power in the “vee" and causes it to heat. If we consider a tiny volumetric element of “vee" material, the current passing through it dissipates power in the form of heat due to losses in the electrical resistance of the element. Because the volumetric power is proportional to the square of the current density, the heat generated in the “vee" reduces at a rate twice as fast as the current density as one moves from the surface, into the conductor. The “ Electric Power Reference Depth" is then half of the “Electrical Reference Depth". The heating by electric power dissipation causes the temperature of the material in the vicinity of the “vee" to rise because of two physical phenomena:

• First, heat generated in the element is stored in its “Heat Capacitance". It is a well understood physical law that the temperature of a volumetric element equals the heat energy contained in it multiplied by its volumetric Heat Capacity.

• Second, adjacent volumetric elements exchange heat in proportion to their temperature difference. This is the well known process of Thermal Conduction.

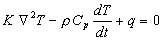3)

Where:

T	is the temperature distribution in the material, ,
q	is the heat generated in the material,
K	is the thermal conductivity of the pipe or tube material,
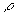	is the density of the material,
Cp	is the heat capacity of the material.

Solution of this equation tells us that when heat is generated in a portion of a thermally conducting piece of material, the temperature rise is instantaneously confined to the region being heated. However as time increases, adjacent material elements experience a temperature rise as the heat spreads out due to thermal conduction. The shape of this temperature distribution at any point in time contains a very abrupt transition between a temperature approaching that of the part of the material being heated and that of the material before it was heated. If a single element of material starts to heat at time t = 0, the location of this temperature transition relative to the heated element can be described by the “Thermal Reference Depth" which increases with time:

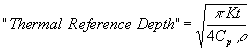4)

To this point in the paper, everything disclosed about the high frequency welding process has been known for some time. What was not understood until recently was the answer to the question:

Is the high frequency welding process governed by electrical “Skin Effect" so that the temperature distribution in the “vee" edge is determined by the “Electric Power Reference Depth" or is it governed by “Thermal Conduction" so that the temperature distribution is determined by the “Thermal Reference Depth"?

The answer is that the process can be controlled by either the “Electric Power Reference Depth" or the “Thermal Reference Depth" depending on the welding frequency, mill speed, and tube product being produced!! The interaction between electrical “Skin Effect" and “Thermal Conduction" has been determined by combining Maxwell's Equations with the Biot-Fourier Equation and solving the two together. The result explains the effect of frequency on the induction tube welding process and reconciles the abnormalities between conflicting experimental data.

The Effect of Frequency on the Power Required to Weld:

The principle result of this new process model is that the power required to heat the “vee" to the forge welding temperature can be accurately predicted from an equation relating welding frequency, mill speed, “vee" length, tube wall thickness, and the electrical and thermal properties of the strip material. The resulting equation is:

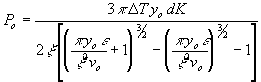5)

Where:

Po	is the power required in the “vee" to weld the pipe or tube, ,
d	is the wall thickness of the pipe or tube,
Vo	is the mill speed,
yo	is the length of the weld “vee",
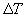	is the forge temperature rise required to weld the material.
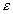	equals K /Cp 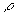which is the thermal diffusivity of the material.

The main feature of this equation is its denominator. Careful examination results in the conclusion that the “Vee" Welding Power Required will assume two completely different characters depending on whether:

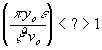6)

Rearranging this expression yields an entirely predictable result:

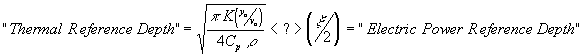7)

or is the Thermal Reference Depth significantly greater or less than the “Electric Power Reference Depth"? From this observation we can define three distinct modes for the operation of the high frequency welding process. We will say that the process is in the “Thermal Mode" if the “Thermal Reference Depth" is significantly larger than the “Electric Power Reference Depth" and we will say that the process is in the “Electric Power Mode" if the “Electric Power Reference Depth" is significantly larger than the “Thermal Reference Depth". If the two reference depths are roughly equal, we will say that the process is in the “Transition Mode". We can use binomial expansion to find results for the “vee" power for each of the process modes. These are:

“Thermal Mode":

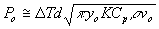8)

“Transition Mode":

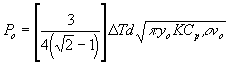9)

“Electric Power Mode":

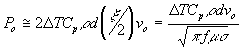10)

These results tell us that when the process is in the “Thermal Mode", the “vee" power requirement is independent of welding frequency. Also, for a given mill speed, tube material, and “vee" length, the power requirement is minimized by operating in the “Thermal Mode". If the process is in the “Transition Mode", the power required is nearly twice the power required in the “Thermal Mode". As the process transitions to the “Electric Power Mode" for a given tube material, the power continues to increase as Also, when the process is in the “Thermal Mode", it has the least sensitivity to changes in mill speed. To double the mill speed, only 41% more power is required. If the process is in the “Electric Power Mode", twice the power is required to double the mill speed. As most of the material properties are under the square root radical, the process is less sensitive to material property variations when it is in the “Thermal Mode". It should be clear that from a weld power viewpoint, it is highly desirable to operate the process in the “Thermal Mode".

Figure 1 shows the results of both experiment and calculation for “vee" power for a specific tube size fabricated at three different mill speeds and welding frequencies from 100 to 425 kHz. As the mill speed is increased from 30 meters per minute to 60 meters per minute then to 90 meters per minute, the process transitions from the “Thermal Mode" to the “Electric Power Mode". As welding frequency is increased, the process operation moves towards the “Thermal Mode". At the slowest mill speed, welding frequency has little effect on the welding power requirement, but at the highest speed, the power requirement changes by 25% between 200 kHz and 400 kHz welding frequency. Figure 1 - Comparison of Experimental and Calculated Power in the Weld "Vee"

Also of interest is the relationship between the total power supplied by the welder and the power required in the “vee" necessary to perform the welding operation. Figure 2 shows data obtained from six operating tube mills at six different tube producers. The quality of the mill set-up varied significantly from mill to mill as did the product produced. Data was collected for both aluminum and steel tube with outside diameters ranging from 11 mm to 127 mm, wall thickness ranging from .73 mm to 5.46 mm, welding frequencies from 300 to 419 kHz, and mill speeds from 3 meters per minute to 150 meters per minute. For each example, the “vee" power required to perform the weld was calculated from equation 5. This data is plotted in Figure 2. Linear regression techniques were used to fit a straight line to the data as is also shown in the figure. The result is that on average the process is 21.5% efficient in that the theoretical “vee" power is on average 21.5% of the power actually supplied by the welder. The remaining 78.5% of the power supplied by the welder is distributed over the tube's surface. This result can be used with the “vee" power equation to estimate the weld power required for cases where prior data does not exist.

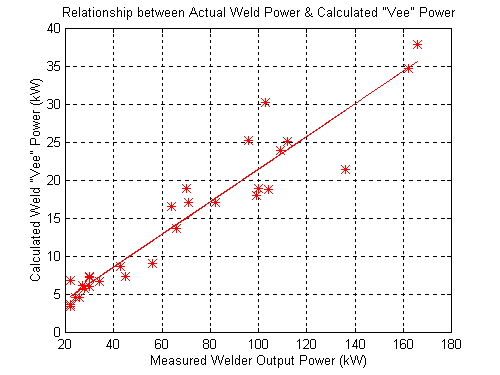Figure 2 - Data for Experimentally Determining Efficiency of the Induction Welding Process

The Effect of Frequency on the Size of the Heat Affected Zone (HAZ):

It is reasonable to expect that the width of the Heat Affected Zone (HAZ) will follow the “Thermal Reference Depth" when the process is in the “Thermal Mode" and the “Electric Power Reference Depth" when the process is in the “Electric Power Mode", as these will determine the respective depth of heating. In the “Transition Mode", the Heat Affected Zone (HAZ) should follow the sum of the two reference depths as then both determine the depth of heating. As the Heat Affected Zone (HAZ) is measured across both sides of the “vee", the appropriate reference depth should be multiplied by a factor of two.

Figures 3 through 5 show the Heat Affected Zone (HAZ) measured from tubing samples taken while performing the weld power measurements shown in Figure 1. Also plotted are twice the “Thermal Reference Depth" and twice the “Electric Power Reference Depth". This data correlates well with the notion that Heat Affected Zone (HAZ) follows the depth of heating as defined by the appropriate reference depth.

Figure 3 - Heat Affected Zone (HAZ) Data at 30.5 Meters per Minute Mill Speed

Figure 4 - Heat Affected Zone (HAZ) Data at 61 Meters per Minute Mill Speed

Figure 5 - Heat Affected Zone (HAZ) Data at 91.5 Meters per Minute Mill Speed

It should be clear that for a particular tube material, mill speed, and “vee" length, the minimum Heat Affected Zone (HAZ) occurs when the process is operated in the “Thermal Mode". When the process is operated in the “Electric Power Mode", more of the pipe or tube material is heated. In addition to using more power, this affects the metallurgical properties of the material over a greater area than when the process operates in the “Thermal Mode".

The Effect of Frequency on the Impeder Magnetic Flux Level:

Welding frequency affects the level of magnetic flux in the impeder in two ways. First, as frequency is increased less flux is required to transfer the same amount of power. This is why the core of a 50 Hz power transformer is larger than the core of a 60 Hz transformer. The second reason is that as the welding frequency is decreased, the process transitions from the “Thermal Mode" to the “Electric Power Mode" and requires more power to weld the same tube at the same mill speed. The increased power transfer requires more flux in the impeder.

The result for “vee" power can be used to calculate the flux level in the impeder because all of the impeder flux must pass through the “vee" area and because the current in the “vee" is directly related to the magnetic field in the “vee" through “Surrogate Proximity". With fCritical as the welding frequency defining the center of the “Transition Mode", the result is that the flux in the impeder can be found from:

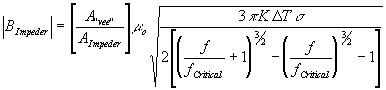11)

Where:

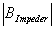	is the magnitude of the magnetic flux in the impeder, ,
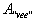	is the area of the weld “vee",
	is the cross-sectional area of the impeder,
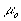	is the magnetic permeability of free space,
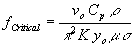	is the welding frequency defining the center of the “Transition Mode"

Limiting cases can be found for when the process is in the “Thermal Mode" and for when the process is in the “Electric Power Mode". These are:

“Thermal Mode" Impeder Flux Level:

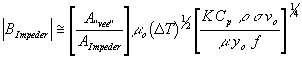12)

“Electric Power Mode" Impeder Flux Level:

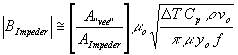13)

It can be seen that impeder flux varies as f-1/2 in the “Electric Power Mode" and reaches its minimum value varying as f-1/4 as the frequency is increased to the point the process is operating in the “Thermal Mode". Again, the most advantageous mode of process operation, the one that keeps the impeder the furthest away from flux saturation, is the “Thermal Mode". By way of example, Figure 6 shows how the impeder flux level varies as a function of frequency when producing typical small tube.

Figure 6 - Impeder Flux as a Function of Frequency Predicted for a Typical Small Tube

The “Optimum" Welding Frequency:

It should be clear that it is most advantageous to operate the pipe and tube, induction welding process in the “Thermal Mode". This mode of operation results in the lowest weld power requirement, the narrowest Heat Affected Zone, and the lowest impeder magnetic flux level. While operation in the “Transition Mode" is more desirable than operation in the “Electric Power Mode" as the weld power and impeder flux will be lower and the Heat Affected Zone (HAZ) narrower, the process will be significantly more sensitive to variations in material properties and process parameters than when it is operated in the “Thermal Mode". Also, the affect of these variations will be different if the process is closer to the “Thermal Mode" or the “Electric Power Mode". When diagnosing process problems, the perception will be “What worked yesterday, doesn't work today".

How can we insure that the process is operated in the “Thermal Mode"? Equation 6 tells us how this may be accomplished. If we start with a particular tube to be produced, the material, and hence its material properties, the tube outside diameter, and wall thickness have been determined. If the mill set-up follows standard practice, the “vee" length will be approximately the tube diameter, D, so we can substitute this into equation 6. We can now solve for the welding frequency that defines the center of the “Transition Mode" for a particular mill speed. We will call this the “Critical Frequency":

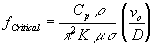14)

Operating the process at a welding frequency significantly above the “Critical Frequency" assures the process is operating in the “Thermal Mode". Operating the process at the “Critical Frequency" places the process in the “Transition Mode". Figure 7 shows the “Critical Frequency" as a function of both tube outside diameter and mill speed for low carbon steel. This chart can be used to determine the “best" welding frequency for a particular mix of tube products and mill speeds. Remember that to keep the process in the “Thermal Mode" for the entire product mix, the highest frequency required to do the complete product mix should be chosen for the welder, if its output frequency is fixed.

Figure 7 - Chart for Determining the "Critical Frequency" for Low Carbon Steel Pipe & Tube

Summary:

A comprehensive theory based on physical laws is now available to determine the affects of welding frequency on the pipe and tube, induction welding process. This theory shows that the process operates in two limiting modes, the “Thermal Mode" and the “Electric Power Mode", and these are connected by a third “Transition Mode". It is most desirable to operate the process in the “Thermal Mode". For a particular tube to be produced and mill speed, this results in:

• The highest consistent pipe and tube quality.
• The lowest welding power requirement.
• The least sensitivity to mill speed and the least additional power required as mill speed is increased.
• The least sensitivity to variation in the material properties of the strip.
• The narrowest Heat Affected Zone (HAZ).
• The lowest impeder magnetic flux level, keeping it as far as possible from saturation

¹ Scott, P. F., Key Parameters of High Frequency Welding, Proceedings of the Tube/Pipe Congress 96, Dusseldorf, Germany, April 16-18, 1996.

For more information, please contact :

Thermatool Corp.
East Haven, CT, USA
Tel: (203) 468-4100
Fax: (203) 468-4281
Email.
Contact. Paul Scott, Vice President, Technology